Teoremas de ternas pitagóricas y ternas
racionales:
Teorema
1:
Si la fórmula de Pitágoras es representada
con las letras ![]() ,
,
![]() y
y ![]() entonces se tiene
entonces se tiene
que:
![]() (1)
(1)
Son ternas pitagóricas ![]() ,
, ![]() y
y ![]()
si y solo si cumplen las siguientes condiciones en los cuatro
casos:
Caso 1:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 2:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 3:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 4:
![]()
![]()
![]()
![]()
![]()
![]() (1.1)
(1.1)
Donde en los cuatro casos: ![]()
![]() y
y ![]()
son enteros tal que![]() y
y ![]() .
.
Demostración:
Para demostrar estos teoremas es necesario expresar la
formula de Pitágoras en la forma:
![]() (2)
(2)
Donde ![]() ,
,
![]() y
y ![]() pertenecen al conjunto de
pertenecen al conjunto de
los enteros, por tanto también:
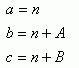 (2.1)
(2.1)
Pertenecen al conjunto de los enteros. Desarrollando los
binomios de la ecuación 2 y simplificando
queda:
![]() (2.3)
(2.3)
Despejando ![]() por medio de la formula general cuadrática se
por medio de la formula general cuadrática se
tiene:
![]()
Simplificando:
![]() (2.4)
(2.4)
Analizando la parte de la raíz de la
ecuación 2.4:
![]()
![]() (2.5)
(2.5)
Hay 4 posibilidades para no tener números
irracionales en 2.5:
Caso 1:
![]()
![]()
Caso 2:
![]()
![]()
Caso 3:
![]()
![]()
Caso 4:
![]()
![]() (2.5.1)
(2.5.1)
Donde ![]()
es un entero tal que
![]()
Cuando ![]()
es entero mayor que cero. Sustituyendo ![]() en las ecuaciones
en las ecuaciones
2.5.1:
Caso 1:
![]()
![]()
Caso 2:
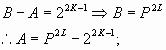
![]()
Caso 3:
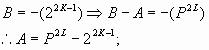
![]()
Caso 4:
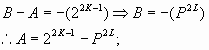
![]() (2.5.2)
(2.5.2)
Donde en los cuatro casos: ![]()
![]() y
y ![]()
son enteros tal que![]() y
y ![]() .
.
Aplicando las ecuaciones 2.5.2 a 2 quedan los casos:
Caso 1:
![]()
Caso 2:
![]()
Caso 3:
![]()
Caso 4:
![]() (2.6)
(2.6)
Simplificando los elementos que se elevan al cuadrado de
2.6 se tienen,
Caso 1:
![]()
Caso 2:
![]()
Caso 3:
![]()
![]()
Caso 4:
![]()
![]()
(2.6.1)
Entonces por las ecuaciones 2.6.1 son ternas
pitagóricas enteras ![]() ,
, ![]() y
y
![]() si y solo si
si y solo si
cumplen las siguientes condiciones:
Caso 1:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 2:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 3:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 4:
![]()
![]()
![]()
![]()
![]()
![]() (2.6.2)
(2.6.2)
Donde en los cuatro casos: ![]()
![]() y
y ![]()
son enteros tal que![]() y
y ![]() , que era
, que era
lo que se quería demostrar.
Observación 1: solamente se cumplen las
igualdades 2.6.2, cuando se toma el elemento ![]() positivo o negativo en
positivo o negativo en
![]() ,
, ![]() y
y ![]() , esto es:
, esto es:
Caso 1:
![]()
Caso 2:
![]()
![]()
Caso 3:
![]()
![]()
Caso 4:
![]()
![]()
O también:
Caso 1:
![]()
Caso 2:
![]()
Caso 3:
![]()
![]()
Caso 4:
![]()
![]()
Teorema 2:
Si la formula de Pitágoras es representada con
las letras ![]()
![]()
![]()
![]()
![]() y
y ![]()
entonces queda:
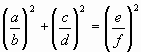 (3)
(3)
Cuando ![]() son ternas racionales
son ternas racionales ![]()
![]() y
y
![]() si y solo si
si y solo si
cumplen las siguientes condiciones:
Caso 1:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 2:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 3:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 4:
![]()
![]()
![]()
![]()
![]()
![]()
Donde en los cuatro casos: ![]()
![]() y
y ![]()
son enteros tal que![]() y
y ![]() .
.
Demostración:
Si la ecuación 3 es multiplicada por ![]() y se simplifica
y se simplifica
queda:
![]() (3.1)
(3.1)
Por definición de número racional se sabe
que los productos
![]()
![]() y
y ![]() son números enteros esto quiere
son números enteros esto quiere
decir que por el teorema 1 son ternas pitagóricas
![]()
![]() y
y ![]() si y solo si cumplen las siguientes
si y solo si cumplen las siguientes
condiciones:
Caso 1:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 2:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 3:
![]()
![]()
![]()
![]()
![]()
![]()
Caso 4:
![]()
![]()
![]()
![]()
![]()
![]() (3.2)
(3.2)
Donde en los cuatro casos: ![]()
![]() y
y ![]()
son enteros tal que![]() y
y ![]() , por lo
, por lo
tanto en la ecuación 3 son ternas pitagóricas
racionales ![]()
![]() y
y ![]() si y solo si cumplen las
si y solo si cumplen las
anteriores condiciones, que era lo que se quería
demostrar.
Estos teoremas pueden servir para demostraciones
geométricas cuando se tiene la figura como varios triángulos pitagóricos, o cuando se
tienen lados racionales. El conjunto de los racionales contiene a
los enteros, por tanto el teorema 1 es un caso particular del
teorema 2.
Ejemplo 1:
Demostrar que no se puede construir un cuadrado cuyos
lados ![]()
![]()
![]()
![]()
![]()
![]()
![]() y
y ![]() , pertenecen al conjunto
, pertenecen al conjunto
de los enteros tal que ![]() (Fig. 1).
(Fig. 1).
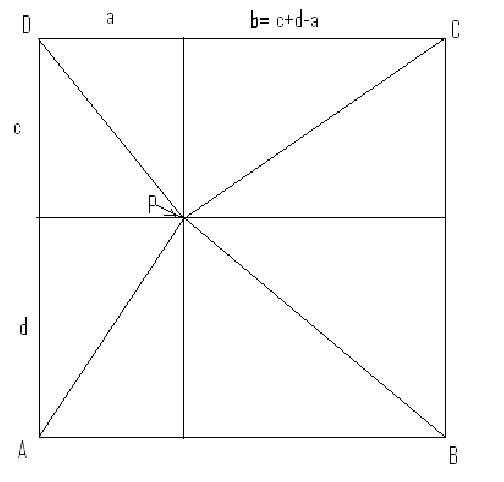
Figura 1.
Demostración: si ![]()
![]()
![]() y
y ![]() , pertenecen al conjunto
, pertenecen al conjunto
de los enteros y ![]()
![]() (4)
(4)
Por el teorema de Pitágoras:
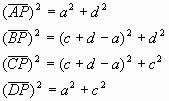 (4.1)
(4.1)
Por el teorema 1, en todos los casos se debe de cumplir
lo siguiente:
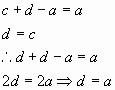
(4.2)
Esto es imposible, ya que para todos los casos y
valores
posibles de ![]()
![]() y
y ![]() siempre se
siempre se
cumplirá:
Caso 1:
![]()
![]()
![]()
![]()
![]()
Caso 2:
![]()
![]()
![]()
![]()
![]()
Caso 3:
![]()
![]()
![]()
![]()
![]()
Caso 4:
![]()
![]()
![]()
![]()
![]()
Que era lo que se quería demostrar.
Ejemplo 2:
Demostrar que no se puede construir un
paralelepípedo rectangular que tiene las
características de que todas sus aristas y todas sus
diagonales miden números enteros (fig.2).
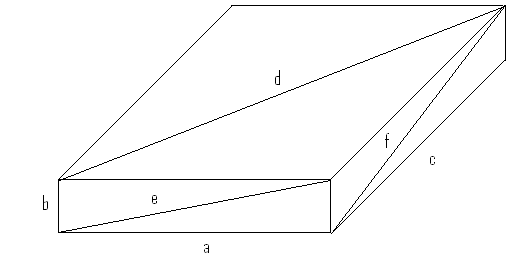
Figura 2.
Demostración: si ![]()
![]()
![]()
![]()
![]() y
y ![]() pertenecen al conjunto de los enteros y
pertenecen al conjunto de los enteros y ![]() por el teorema de
por el teorema de
Pitágoras se tienen las igualdades:
![]()
![]() (5)
(5)
![]()
Por el teorema 1 en cualquier caso se debe cumplir
que:
![]() (5.1)
(5.1)
Aplicando 5.1 en 5 también se debe de
cumplir:
![]()
Igualdad que por hipótesis es absurda, como se quería
demostrar.
Referencias:
[1] Apóstol, T. M. (1984/2002).
Introducción a la teoría de números. (2ª
Reimpresión, p.4). Sevilla: Reverte, S.A.
Diego Galván Caldera
Tecnólogo
Estudiante de licenciatura en física de cuarto
semestre en el Centro de Ciencias
Exactas e Ingenierías (CUCEI), Universidad de
Guadalajara
Tecnólogo Diego Galván Caldera, egresado
del Centro de Enseñanza Técnica Industrial (CETI),
de la carrera de Maquinas-Herramienta.
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |
